|
Lineare Gleichungen
[lineare Gleichungen mit
einer Unbekannten] [lineare
Gleichungen mit zwei Unbekannten]
Linearen
Gleichungen mit einer Unbekannten
→ allgemeine Form: ax + b = 0
(a, b, x
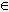 R) R)
------------------------------
Lösung einer linearen
Gleichung der Form ax + b = 0:
Äquivalente Umformungen einer linearen Gleichung:
Umformungen, die die Lösungsmenge der Gleichung unverändert
lassen.
z. B.:
- auf beiden Seiten der Gleichung dieselbe Zahl addieren
- auf beiden Seiten der Gleichung dieselbe Zahl
subtrahieren
- beide Seiten der Gleichung mit derselben (von Null
verschiedenen) Zahl multiplizieren
- beide Seiten der Gleichung durch dieselbe (von Null
verschiedene) Zahl dividieren
- beide Seiten der Gleichung potenzieren (z. B.
quadrieren)
- aus beiden Seiten der Gleichung die Quadratwurzel ziehen
Wann gilt eine (lineare) Gleichung als gelöst?
Für die Unbekannte (z. B. x) gilt:
- x muss im Zähler stehen
- x darf nur auf einer Seite der Gleichung stehen
- x muss allein dort stehen
(also nur: 1x =)
- x muss positiv sein
(also: +x =)
Hinweis zur Lösung einer Gleichung:
- Störglieder werden immer durch die entgegengesetzte
Rechenoperation beseitigt (auf die andere Seite der Gleichung gebracht)
Beispielaufgaben:
(ausführlicher Rechenweg)
(1) (2)
| 8x = 48 |
| :
8 |
10x + 8 = 6x + 16 |
| -
8 |
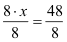 |
(Kürzen) |
10x +
8 - 8 = 6x + 16 -8
10x = 6x + 8 |
(Zusammenfassen) | - 6x |
|
x = 6 |
(Ergebnis) |
10x - 6 x = 6x + 8 - 6x
4x = 8 |
(Zusammenfassen) |: 4 |
| |
|
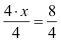 |
(Kürzen) |
| |
|
x = 2 |
(Ergebnis) |
(3)
| 5 +
4x + 8 - x = x + 22 + x |
(Zusammenfassen) |
|
13 + 3x = 2x + 22 13 + 3x - 13 = 2x + 22 - 13 |
| - 13 (Zusammenfassen) |
|
3x = 2x + 9
3x - 2 x = 2x + 9 - 2x |
| - 2x (Zusammenfassen) |
|
x = 9 |
(Ergebnis) |
(kurzer Rechenweg)
(4) (5)
| 12y = 84 |
| :
12 |
2a
+10 + 5a -15 = 3a +7 |
(Zusammenfassen) |
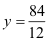 |
(Kürzen) |
7a - 5 = 3a +7
4a - 5 = 7 |
| - 3a | + 5 |
| y = 7 |
(Ergebnis) |
4a = 12 |
| : 4 |
| |
|
a = 3 |
(Ergebnis) |
Übungsaufgaben:
Löse folgende lineare Gleichungen!
- 7x = 49
- 8y = 88
- 16 = 4z
- 15x + 16 = 31
- 12a - 32 = 4
- 45 = 5z - 15
- 4x + 9 + 3x - 14 = 3x + 7
- 6x + 3 = 2x + 11
- 14x + 13 = 62 + 7x
|
- 26 + 28x = - 16 + 14x + 140
- 5 + 2x + 8 + x = x + 22 + x
- 8x + 7 = 5x - x + 23
- 7x + 5 - 3x = 15 - 4x + 6
- 6x - 45 - x + 30 - 4x + 17 = 22
- 2x + 3 + 5x = 19 - 6x + 10
- - 9x - 8 + 4x = 28 - 2x - 42
- 15x + 9 - 12 - 18x + 26x = - 54x + 6 + 8 + 31x + 6
- - 108 + 12 + 62x + 28 = 30x + 15 + 18 - 24 - 36x - 15 + 42x
|
Lösungen_1
Lineare Gleichungen mit zwei Unbekannten
Problem:
In der Diätküche einer Klinik werden Mahlzeiten zubereitet, die nur eine
vorgeschriebene Zahl von Joule enthalten dürfen.
Stelle aus Schweinefleisch und Kartoffeln zwei verschiedene Mahlzeiten mit je
1680 J zusammen, wenn man für 100 g Schweinefleisch 504 J und für 100 g
Kartoffeln 336 J ansetzt!
Gleichung:
504x + 336y = 1680 (Dabei sind x = 100 g
Schweinefleisch und y = 100 g Kartoffeln.)
Lösen durch Probieren!
- x = 2
→
200 g Schweinefleisch
y = 2 →
200 g Kartoffeln
- x = 3
→ 300 g
Schweinefleisch
y = ½ →
50 g Kartoffeln
u. a. (→
Es gibt unendlich viele Lösungen.)
→ allgemeine
Form: ax + by + c = 0
(a, b, c, x, y
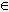 R) R)
Beispiel:
4x - 2y + 2 = 0 Finde
wenigstens 2 Lösungen durch Probieren!
- x = 0
y = 1
L1 = [0;1]
|
- x = 2
y = 5
L2 = [2;5]
|
Weitere Lösungen durch Überlegung
→ Umformen
der Gleichung
4x - 2y + 2 = 0
→
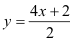 →
y = 2x + 1
→
y = 2x + 1
Ermittlung weiterer Lösungen mit Hilfe einer Wertetabelle:
|
Y = 2x+1 |
x |
|
3 |
1 |
|
7 |
3 |
|
-1 |
-1 |
|
-3 |
-2 |
|
2 |
0,5 |
|
0 |
-0,5 |
|
Weitere Lösungen: L3 = [1;3]
L4 = [3;7]
L5 = [-1;-1]
L6 = [-2;-3]
L7 = [0,5;2]
L8 = [-0,5;0] |
Grafische Darstellung aller Lösungen:
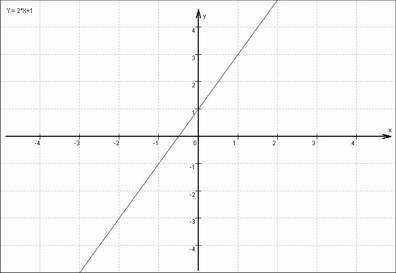 |
Die lineare Gleichung 4x - 2y + 2 = 0 hat unendlich viele
Lösungen. Die Lösungsmenge ist eine Gerade. |
Übungen:
- Löse folgende lineare Gleichungen grafisch und gib wenigstens jeweils 2
Wertepaare als Lösung an!
a) x - 2y = -5
b) 4x = 3 + 2y
c) 3x - 4y = 1
- Welche der gegebenen Paare rationaler Zahlen sind Lösung der linearen
Gleichung 7x - 4y = 3?
| a) [1;1] |
b) [3;4] |
c) [-2;-4] |
d) [0;-3/4] |
Lösungen_2
|