|
Lineare
Gleichungssysteme mit 2 Unbekannten
|
Problem: |
Die Dekorationsabteilung eines
Kaufhauses bestellt beim Fachhandel 50 Kunstblumen, die
sowohl in Draht (80 g) als auch in Plastik (30 g)
lieferbar sind. Der Lieferant möchte die Sendung durch
die Post zustellen.
Wie viele Drahtblumen dürfen dabei sein, damit das
zulässige Höchstgewicht für das Päckchen von 2 kg
ausgenutzt, aber nicht überschritten wird? |
Lösung: |
|
|
| Annahme: |
x .... Drahtblumen |
y .... Plastikblumen |
| lineare
Gleichung für die Stückzahl: |
x + y = 50 |
→
y = 50 - x |
| lineare
Gleichung für das Gewicht: |
80x + 30y = 2000 |
→
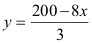 |
Wie kann man das Problem lösen?
1 zeichnerisch
2 rechnerisch
3 mit Hilfe von Determinanten und Matrizen
1 zeichnerische Lösung
Wertetabellen:
Stückzahl:
|
Y = 50 - x |
x |
|
50 |
0 |
|
40 |
10 |
|
30 |
20 |
|
20 |
30 |
|
10 |
40 |
|
0 |
50 |
Gewicht:
|
Y = (200 - 8x)/3 |
x |
|
66,7 |
0 |
|
40,0 |
10 |
|
13,3 |
20 |
|
0 |
25 |
|
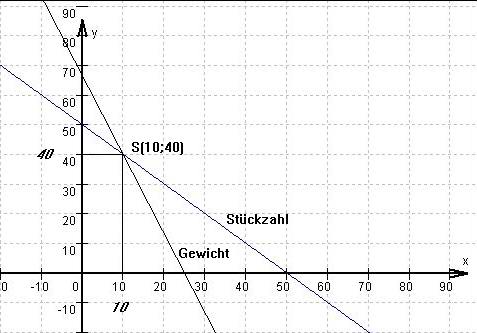 |
Ergebnis:
Aus der grafischen Darstellung erhält man folgende
Koordinaten für den Schnittpunkt S der beiden Geraden: S(10;40).
→ x = 10
y = 40
Frage:
Gibt es mehr Lösungen?
→
NEIN
Antwort:
Die Postsendung muss aus 10
Drahtblumen und 40 Plastikblumen bestehen, damit das
Transportgewicht ausgenutzt, aber nicht überschritten wird.
2 rechnerische Lösung
I. x + y = 50
II. 80x + 30y = 2000
Wie kann man ein
System aus 2 Gleichungen mit 2 Unbekannten rechnerisch lösen?
|
 |
Es gibt insgesamt 3 Lösungsverfahren:
- Einsetzungsverfahren
- Gleichsetzungsverfahren
- Additionsverfahren
|
|
A.
Das Einsetzungsverfahren
|
→ |
Eine
Gleichung des Gleichungssystems nach einer beliebigen
Variablen auflösen und den erhaltenen Term für diese
Variable in der anderen Gleichung einsetzen. |
I. x + y = 50
→
x = 50 - y
(z.
B. Gleichung I nach x auflösen)
II. 80x + 30y = 2000
I in II einsetzen:
|
80(50 - y) + 30y = 2000
4000 - 80y + 30y
= 2000
4000 - 50y = 2000
2000 = 50y
40 = y
(Plastikblumen) |
Berechnung von x (Drahtblumen) durch
Einsetzen in Originalgleichung: I.
x + 40 = 50
x = 10 |
Probe:
I. 10 + 40 = 50
II. 80 * 10 + 30 * 40 = 2000
50 = 50
800 + 1200 = 2000
2000 = 2000
→ [10;40] ist die Lösung des
gegebenen linearen Gleichungssystems
→ Lösungsmenge: L = {10;40}
Ergebnis:
Die Postsendung muss aus 10
Drahtblumen und 40 Plastikblumen bestehen, damit das
Transportgewicht ausgenutzt, aber nicht überschritten wird.
B.
Das Gleichsetzungsverfahren
|
→ |
Beide
Gleichungen des Gleichungssystems nach derselben
Variable auflösen und die erhaltenen Terme
gleichsetzen. |
I. x + y = 50
→
x = 50 - y
II. 80x + 30y = 2000
→
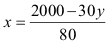
I = II:
50 - y =
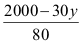
80(50 - y) = 2000 - 30y
4000 - 80y = 2000 - 30y
2000 = 50y
40 = y
(Plastikblumen) |
Berechnung von x (Drahtblumen) durch
Einsetzen in Originalgleichung: I.
x + 40 = 50
x = 10 |
→ [10;40] ist die Lösung des
gegebenen linearen Gleichungssystems
→ Lösungsmenge: L = {10;40}
Ergebnis:
Die Postsendung muss aus 10
Drahtblumen und 40 Plastikblumen bestehen, damit das
Transportgewicht ausgenutzt, aber nicht überschritten wird.
C.
Das Additionsverfahren
|
→ |
Eine
Gleichung des Gleichungssystems durch Umformen so
geschickt erweitern, dass sich bei der Addition
der beiden Gleichungen eine Unbekannte aufhebt. |
I. x + y = 50
|
Gleichung mit (-80) erweitern
→
- 80x - 80y = - 4000
II. 80x + 30y = 2000
I + II:
|
- 80x - 80y + 80x +
30 y = - 4000 + 2000
- 50 y = - 2000
y = 40
(Plastikblumen) |
Berechnung von x (Drahtblumen) durch
Einsetzen in Originalgleichung: I.
x + 40 = 50
x = 10 |
→ [10;40] ist die Lösung des
gegebenen linearen Gleichungssystems
→ Lösungsmenge: L = {10;40}
Ergebnis:
Die Postsendung muss aus 10
Drahtblumen und 40 Plastikblumen bestehen, damit das
Transportgewicht ausgenutzt, aber nicht überschritten wird.
3
mit Hilfe von Determinanten und Matrizen
I. x + y = 50
II. 80x + 30y = 2000
Hinweis:
Jede Gleichung des linearen Gleichungssystems muss die Form
ax + by = c
besitzen!
Cramersche Regel:
Wenn die Koeffizientendeterminante D eines linearen
Gleichungssystems ≠ 0 ist, besitzt
dieses genau eine Lösung.
Lösung:
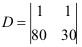 →
→
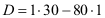 →
D = -50
→
D = -50
→ [10;40] ist die Lösung des
gegebenen linearen Gleichungssystems
→ Lösungsmenge: L = {10;40}
Ergebnis:
Die Postsendung muss aus 10
Drahtblumen und 40 Plastikblumen bestehen, damit das
Transportgewicht ausgenutzt, aber nicht überschritten wird.
Übung:
Löse folgende lineare
Gleichungssysteme:
a)
I. 2x + y = 4
II. x + 2y = 5
durch das
Gleichsetzungsverfahren |
b)
I. 6x + 4y = 24
II.
x - y = 2durch
das Einsetzungsverfahren |
c)
I. 2x + 3y = 12
II. 3x - 2y = 5
durch das
Additionsverfahren |
d)
I. 2y - 4 = 6x
II. 2x - y = 5
mit Hilfe der
Koeffizientenmatrix und der Determinante D |
e)
I. 23x - 32 = 7x - 8y
II. 6x
- 6y = y - 8x
freie Wahl
|
f)
I. y - 3x = 1
II. 3x + y = 7
grafisch
|
Lösungen |