|

Schülermosaik
Infothek "Liebe"
Infos für Schüler
Hilfen und Übungen in Mathematik
Hilfen und Übungen in Deutsch
Kaufmännischer Schriftverkehr
Tabellenkalkulation mit Excel
Referate &
Dokumentationen
Kreativ schreiben
Poesiesprüche
Wer-Was-Wie-Warum?
Mode & Outfit
Berufe-Online
Schülermosaik
Impressum
Gondrams Rainbowpage
Magie & Mythen
Infothek "Liebe"
Entstehung von "Rainbow"
Ehemalige Chefredakteure von "Rainbow"
Interview mit
Christiane M.
(Mitbegründerin und
1. Chefredakteurin von "Rainbow")
Aus dem
Leben einer Chefredakteurin ...
(Marina K. - über 4 Jahre Chefredakteurin von
"Rainbow"
Referenzen & Aktivitäten von "Rainbow"

©
Peter Otto
schuelermosaik.de
|
Geometrische
Grundkonstruktionen
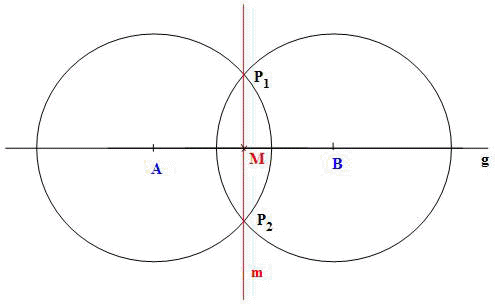
Beschreibung der Konstruktion:
- Jeweils Kreisbögen um A und B mit einem Radius, der größer als die
halbe Strecke AB ist, schlagen.
- Die Verbindungslinie durch die Schnittpunkte P1 und P2 der beiden Kreisbögen
schneidet die Strecke AB genau im Mittelpunkt M.
- Diese Verbindungslinie ist gleichzeitig
Mittelsenkrechte m zur Strecke AB.
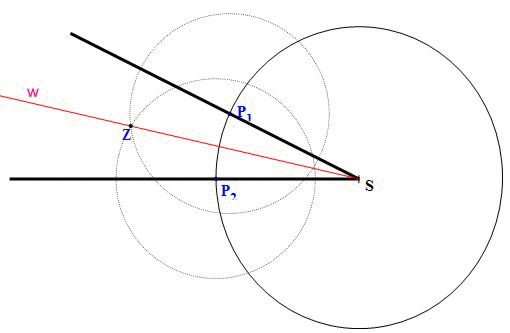
Beschreibung der Konstruktion:
-
Einen Kreisbogen mit beliebigem Radius um den Scheitelpunkt S des
Winkels α schlagen.
-
Um die beiden entstandenen Schnittpunkte
P1 und P2
mit den Winkelschenkeln jeweils einen beliebigen, aber gleichen Radius
schlagen.
-
Die Verbindungslinie durch den so
entstandenen Schnittpunkt Z und den Scheitelpunkt ist die
Winkelhalbierende w des gegebenen
Winkels α.
- Senkrechte zu einer Gerade im Punkt P
errichten
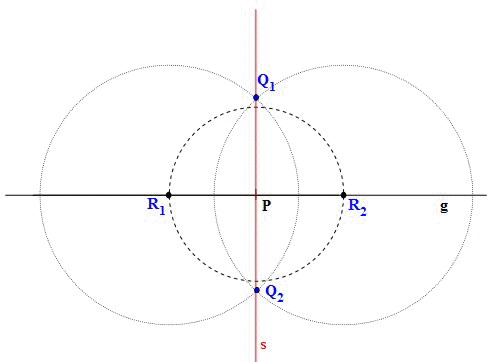
Beschreibung der Konstruktion:
- Kreisbogen mit beliebigem Radius um P schlagen, der die Gerade g in
zwei Punkten R1 und R2 schneidet.
- Um die beiden entstandenen Punkte R1 und R2 jeweils einen Kreisbogen mit
beliebigem Radius schlagen, der aber größer als die halbe Strecke zwischen
den beiden Punkten ist.
- Die Verbindungslinie zwischen den beiden entstandenen Schnittpunkten Q1
und Q2
der beiden Kreisbögen ist die gesuchte Senkrechte
s
zur gegebenen Gerade g durch den Punkt P.
- Lot von einem Punkt P auf eine Gerade g errichten
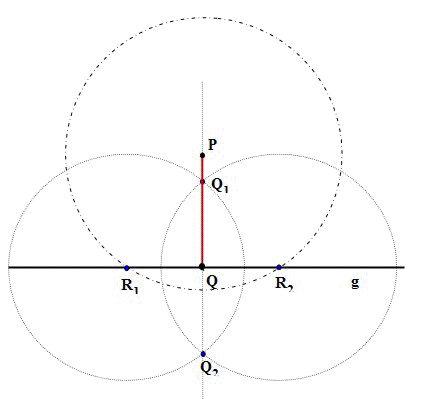
Beschreibung der Konstruktion:
- Kreisbogen mit beliebigem Radius um P schlagen, der die Gerade g in
zwei Punkten R1 und R2 schneidet.
- Um die beiden entstandenen Punkte R1 und R2 jeweils einen Kreisbogen mit
beliebigem Radius schlagen, der aber größer als die halbe Strecke zwischen
den beiden Punkten ist. Diese Kreisbögen schneiden einander in den Punkten
Q1 und Q2.
- Die
Strecke PQ ist das gesuchte Lot von P auf die
Gerade g.
- An einen Kreis von einem Punkt P
außerhalb des Kreises die Tangenten an den Kreis konstruieren
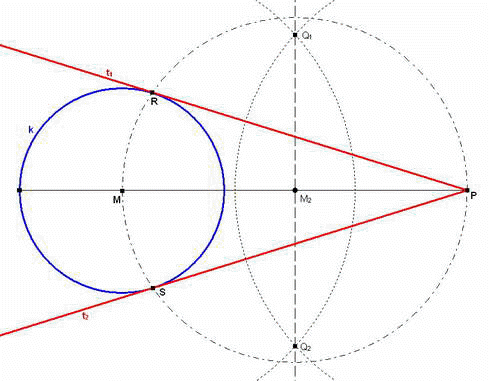
Beschreibung der Konstruktion:
- Um die beiden Punkte M und P jeweils einen Kreisbogen mit
beliebigem Radius schlagen, der aber größer als die halbe Strecke zwischen
den beiden Punkten ist.
- Die Verbindungslinie zwischen den beiden entstandenen Schnittpunkten Q1
und Q2 der beiden Kreisbögen schneidet die Strecke MP genau
im Mittelpunkt M2.
- Kreisbogen mit dem Radius M2P um M2 schlagen.
Dieser Kreisbogen schneidet den gegebenen Kreis k mit dem Radius M in
den Punkten R und S.
- Die Verbindungslinie (Halbgerade) zwischen P und R bzw. P und S sind
die Tangenten t1 und t2
vom Punkt P an den Kreis k.
- Konstruktion des Kreismittelpunktes M
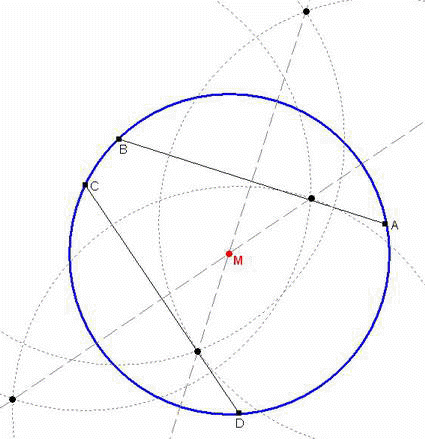
Beschreibung der Konstruktion:
- Zwei beliebige Sehnen AB und CD in den Kreis zeichnen, die verschieden
vom Durchmesser sind.
- Zu den Sehnen AB und CD jeweils die Mittelsenkrechten errichten.
- Diese Mittelsenkrechten schneiden einander im Punkt M. Dieser
Schnittpunkt ist der gesuchte Mittelpunkt M
des gegebenen Kreises.
- Tangente im Punkt P an einen Kreis
errichten
- Der Umkreis eines Dreiecks
- Der Inkreis eines Dreiecks
|

